Lexicographic Ordering in SNMP
What is Lexicographical Order?
In the context of SNMP testing and networks, lexicographical order refers to the specific ordering of variables or objects within a Management Information Base (MIB). It is a hierarchical arrangement where each variable is assigned a unique identifier based on its position in the MIB tree. Lexicographical order determines the sequence in which variables are accessed, allowing for efficient navigation and retrieval of SNMP information. As a network professional, understanding lexicographical order is crucial for effectively managing and troubleshooting SNMP-based devices in your network infrastructure.
Why should I care about lexicographic ordering?
Lexicographic ordering stands as a linchpin within SNMP (Simple Network Management Protocol), and its importance cannot be overstated. This concept might appear as a mere technicality, but it forms the bedrock of accurate information retrieval in SNMP operations like GETNEXT and GETBULK. Its gravity lies in ensuring that the right data is acquired from network devices, and herein lies a crucial message that often gets muffled in the noise of technical discourse.
Imagine the lexicographic ordering as the dictionary-like sequence that the MIB (Management Information Base) adheres to. Now, ponder the domino effect if this sequence is jumbled or misaligned. What seems like a minor glitch can lead to major disruptions. The problem lies in precision, and it's no minor detail. Consider variables related to error counts: retrieving the wrong one could lead to incorrect zero values instead of the real count. This misinformation might cascade into unaddressed network issues and further performance degradation. The point of this narrative is not about merely being precise; it's about ensuring accurate decisions based on accurate data.
In real-world scenarios, the implications are substantial. A network management application might retrieve faulty data due to incorrectly implemented lexicographic ordering. The risk is that this incorrect data will influence decisions that can have profound consequences. This isn't merely about satisfying the technical gods; it's about accurate decision-making in a world where networks govern the flow of information. While the article might not have articulated this point with utmost clarity, the underlying message is that lexicographic ordering isn't a trivial technicality; it's the linchpin that ensures reliable communication between management and network devices.
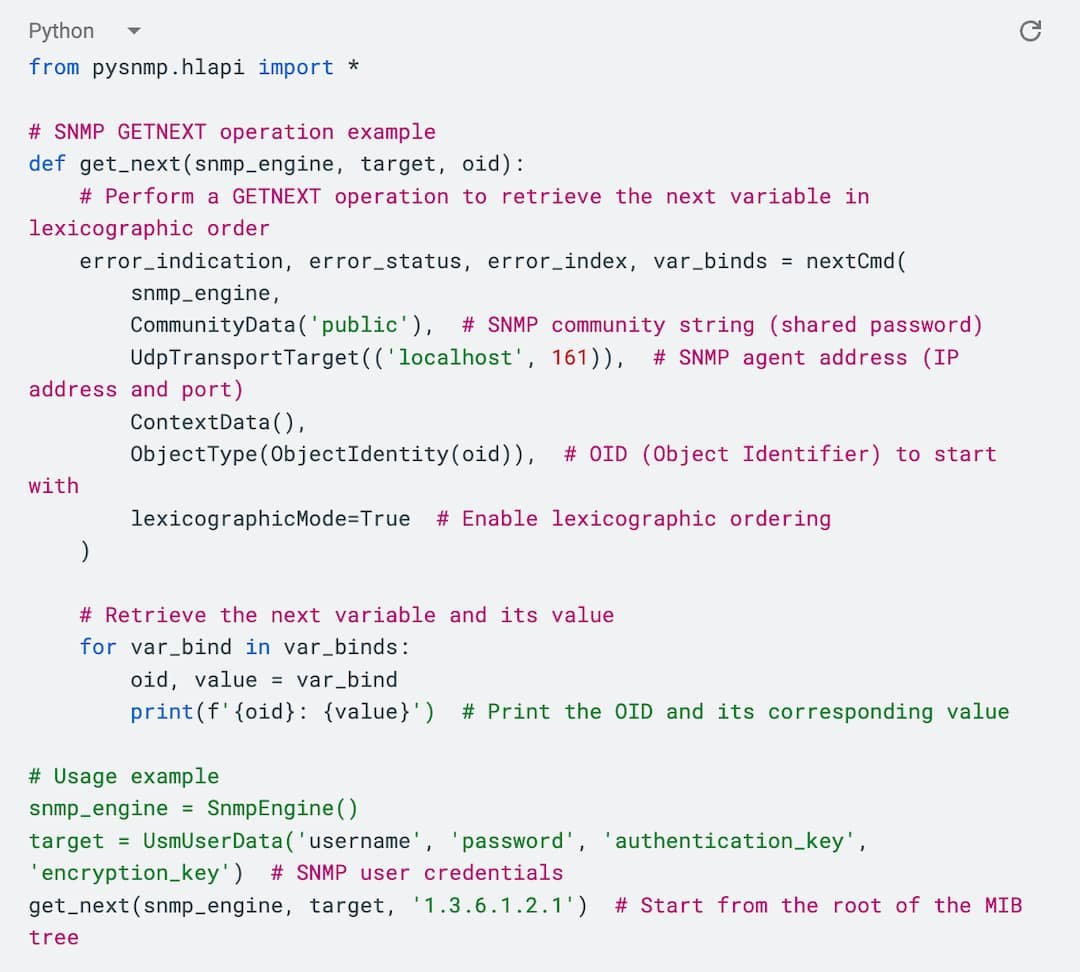
Lexicographic Order Code Example
Lexicographic Python Code Example - Generated by AI
The code above performs a MIB walk using the PySNMP Lib.
For more information on PySNMP
To understand this body of code, keep in mind the following:
lexicographicMode - walk the SNMP agent’s MIB until the end (if True); otherwise (if False), stop the iteration when all response MIB variables leave the scope of the initial MIB variables in varBinds. The default is True.
In other words, if lexicographicMode=True, the lexicographic ordering error in the data sent back by the SNMP agent would be ignored, and the PySNMP lib would try to avoid getting into an infinite loop internally until the MIB walk reaches the end.
If lexicographicMode=False, then PySNMP lib would stop the MIB walking when a lexicographic ordering error is detected in the data sent back by the SNMP agent.
Lexicographic Ordering Sequences
You should care about lexicographic ordering because it is required by GETNEXT and GETBULK operations. See RFC 1157 section 4.1.3 for SNMPv1 operations. See RFC 1905 section 4.2.2 for SNMPv2 GETNEXT and section 4.2.3 for SNMPv2 GETBULK.
Given two sequences,
S=(s(1), s(2), ...s(p))
(it has "p" elements)
T=(t(1), t(2), ... t(q))
(it has "q" elements)Note that an OID value is a sequence of non-negative integers, and that "names of objects" (as specified in RFC 1157 and 1905) are OID values.
Sequence S is lexicographically equal to sequence T if the lengths are equal (that is, p=q) and:
for all i<=p, s(i)=t(i)Sequence S is lexicographically less than sequence T if either of the following are true:
(1) p < q, and for all i <= p, s(i)=t(i)
(2) there exists an i such that (i<=p) & (i<=q), s(i) < t(i) and for all j < i, s(j)=t(j)
© 2021 InterWorking Labs, Inc. dba IWL. ALL RIGHTS RESERVED.
Web: https://iwl.com
Phone: +1.831.460.7010
Email: info@iwl.com